Accostage (Docking) en robotique Mobile
Dans certains environnements, les robots mobiles ont besoin de s’amarrer et/ou d’accoster des objets ou des docks de chargement ou déchargement. La position finale et l’orientation du robot doivent être convenables par rapport à la précision requise pour ce genre de taches.
L’action d’accoster peut être définie simplement comme un mouvement d’une position courante jusqu’à une position et une orientation désirées, en suivant une trajectoire sécurisée. On peut diviser cette tache en trois sous problèmes :
– Se déplacer jusqu’à la position souhaitée tant qu’il n’y a pas risque de collision.
– Progresser avec précision au plus près de la position prévu.
– Effectuer l’accostage
Deux mouvements sont à prendre en compte :
1. Navigation : le véhicule suit une trajectoire libre
2. Accostage : le robot suit une courbe menant au point d’accostage (goal point)
1/ Accostage par Calcul d’un point de retrait.
La méthode est simple : il suffit de calculer un point en retrait par rapport au but à atteindre, ce point doit être décalé d’un angle correspondant à la manœuvre à effectuer et en tenant compte de la largeur du robot. Bien entendu, il est des orientations particulières pour lesquelles cette fonctionnalité n’est pas judicieuse. On peut alors définir des conditions particulières d’utilisation.
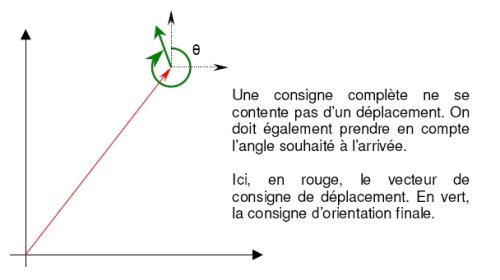
Restrictions :
– Le vecteur de déplacement doit être suffisamment important pour que la modification de trajectoire ne soit pas trop sensible.
– Si l’angle final est égal à l’opposé de l’angle du vecteur de déplacement, à une variation près. Cela revient à rouler sur l’objectif avant de se placer. C’est souvent
inutile de prendre des précautions.
Ces restrictions, sous forme mathématique s’expriment par :
dx²+dy² > Vmin. Vmin représente le module minimum du vecteur de déplacement au carré.
[α-μ+π ; α+μ+π]. μ représente l’ouverture d’angle à éviter.
Calcul du point de retrait C : le vecteur de retrait est calculé sur une base de longueur fixe Vret, et une orientation égale à l’orientation finale souhaitée.
Vretx = Vret.sin(θ)
Vrety = Vret.cos(θ)
Cx = dx - Vret.sin (θ)
Cy = dy - Vret.cos(θ)
La longueur Vret est à déterminer, bien entendu, toujours dans le système d’unité du robot.
Pour effectuer cette trajectoire, on réalisera les éléments suivant :
1. Calcul du point C.
2. Si nécessaire modification d’orientation vers le point C.
3. Si nécessaire, re-calcul des points C et objectif final (point et angle) une fois la modification d’orientation effectuée.
4. Déplacement vers le point C.
5. Calcul du nouvel angle θ et du nouvelles coordonnées du point final dans la base du robot en C.
6. ré-Orientation dans l’angle θ.
7. Calcul des coordonnées du point final.
8. Déplacement vers le point final.
C’est sympa et simple à comprendre mais très couteux à mettre en œuvre et au final pas tellement efficace.
2/ L’algorithme "Pure Pursuit " :
Cette algorithme a été développé pour permettre le suivi d’une trajectoire prédéfinie, avec un maximum d’efficacité. (Il est considéré comme le meilleur algorithme dans ce domaine)
Il consiste à calculer la courbe (arc de cercle) qui passe par la position courante du robot jusqu’à la position désirée (ou une position intermédiaire ).
Le point principal de cet algorithme est de choisir un position intermédiaire qui est à une certaine distance sur le trajet en direction du but à atteindre. Une analogie possible est un conducteur qui regarde un endroit en avant de la voiture et ensuite a tendance à se diriger progressivement vers cet objectif. Cette algorithme est généralement utilisé pour calculer les erreurs de cap par rapport à une trajectoire planifiée.
La courbe utilisée est un cercle, ceci afin de n’avoir qu’un seul looka point possible.
Les coordonnées sont données par rapport au repère du véhicule (Ceci afin que l’algorithme fonctionne correctement). Donc, toutes les coordonnées doivent être transformées dans le repères du véhicule.
L’axe Y : est l’axe formé par la droite passant par le milieu du véhicule dans le sens de déplacement.
L’axe X : passe par le milieu du véhicule perpendiculairement au sens de déplacement et vers la droite.
Soit (xr,yr) la position courante du véhicule, et (xg,yg) le but a convertir dans le repère du véhicule.
Alors :
xgv = (xg - xr)cos(Φ) + (yg-yr)sin(Φ)
ygv = -(xg - xr)sin(Φ) + (yg-yr)cos(Φ)
Où (xgv,ygv) sont les coordonnées du but dans le repère du véhicule et Φ est le cap courant du véhicule.
D est la distance entre le centre du véhicule et le but. 1/γr est le rayon du cercle qui passé par le centre du véhicule et le but.
La courbure de la trajectoire de déplacement du véhicule est calculée comme suit :
γr = 2Δx/D²
Cette équation est obtenue en utilisant les équations suivantes :
1) x² + y² = D²
2) x + d = r
(x,y) sont les coordonnées du but. Un p’tit coup de Pythagore :
d = r - x
(r - x)² + y² = r²
r² - 2rx + x² + y² = r²
2rx = D²
r = D²/2x
γr = 2x/D²
Au final, voici les étapes à suivre afin de réaliser l’algorithme :
1. Obtenir la position du véhicule
2. Trouver le but :
2.1. Calculer le point sur le trajet le plus proche du véhicule (xc, yc)
2.2. Calculer une look-ahead distance D
2.3. Obtenir les coordonnées du but en se déplaçant d’une distance D sur le chemin (trajet) a partir du point (xc,yc)
3. Transformer les coordonnées du but dans le repère du véhicule
4. Calculer la courbure γ = 2Δx/D²
5. Déplacer le véhicule jusqu’au but avec sur le long de la courbe
6. Calculer une nouvelle position et recommencer au point 2.
Le look-ahead (looka) point est un point sur le chemin à une certaine distance D en avant à partir de la projection orthogonale de la position du véhicule sur le chemin.
Changer le look-ahead distance a des effets significatifs sur les performances de l’algorithme.
Augmenter la valeur de L tend à réduire le nombre d’oscillations, pour un suivie de chemin plus linéaire. A contrario, les courbes du chemin les plus refermées auront tendance à être coupées.
En fait, modifier ce paramètre sera une question de contexte. Il y a deux problèmes à considérer :
– Joindre le chemin
– Suivre le chemin.
L’idée de départ était d’utiliser cet algorithme pour faire de l’accostage ou docking (in english). En effet, après avoir passé des heures sur Internet à la recherche de la solution miracle et évidente (que je n’ai pas trouvée), je me suis intéressé à cet algo qui m’avait l’air extrêmement compliqué, mais en même temps, très puissant. Une fois que j’ai réussi à comprendre le fin mot de l’histoire, il était dommage de ne pas en faire profiter tout le monde (c’est toujours du temps gagné).
J’ai modifier un code processing pour faire une démo de l’algorithme pure pursuit.
Un waypoint est calculé en retrait du but et dans la direction opposé au but, a une distance suffisante pour tenir compte du rayon de braquage du robot. Le but est symbolisé par un cercle avec une barre bleu donnant l’orientation de ce dernier.
Le plus grand cercle indique le looka point que le robot cherche a atteindre, le cercle indique la distance D.
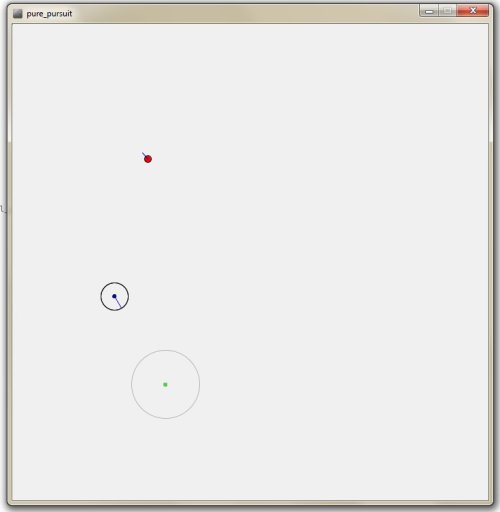
Voici le code processing de la simulation.
3/ Accostage en Logique Floue :
La position et l’orientation du robot sont calculés en temps réel par le module d’odométrie. Les sorties du régulateur flou sont la vitesse de translation et l’orientation que doit avoir le robot (pour nous se sera la vitesse différentielle de la roue droite et gauche), pour atteindre le but désiré selon l’orientation désirée.
L’erreur angulaire est un angle E_Ang, il est calculé en soustrayant l’angle d’accostage, de l’orientation courante du robot. De la même manière que l’on calcule l’erreur de positionnement.
– Dx = Dock.x - position courante robot.x
– Dy = Dock.y - position courante robot.y
– E_Pos= (Dy²+Dx²)1/2
– E_Ang= Angle d’accostage - Orientation courante du robot
Les fonctions de transfert n’ont rien de très exotique, comme d’habitude il faut apporter un peu d’attention pour les adapter à la forme et au mode de déplacement du robot. Les règles d’inférences sont universelles, le tableau permet de les retranscrire assez rapidement dans le code.

Glossaire :
– P Petite
– F Faible
– G Grande
– M Moyenne
– PP Positive Petite
– PG Positive Grande
– TG Très Grande
– NG Négative Grande
– NM Négative Moyenne
– NP Négative Petite
– PM Positive Moyenne
Comme on peut le constater finalement, ce n’est pas bien méchant, merci la logique Flou.
Une petite explication s’impose sur le fonctionnement exact des règles d’inférences :
– Plus on sera loin du but, plus le potentiel sur la position sera fort, donc le robot va surtout chercher à se rapprocher.
– A contrario, plus on sera prés du but, plus l’orientation du robot sera prépondérante, donc il va surtout essayer de s’orienter dans la direction souhaitée.
Attention cela ne veut pas dire qu’il va soit s’orienter soit se déplacer, mais qu’il va effectuer un mixage plus ou moins important de l’un ou de l’autre, en fonction des contraintes (orientation et distance).
Pour ceux qui aurait un robot dont le déplacement est piloté par la vitesse différentiel des roues principales, voici les consignes moteur à appliquer :
– Moteur droit = vitesse + orientation
– Moteur gauche = vitesse - orientation
4/ Calcul de la position du robot pendant son déplacement
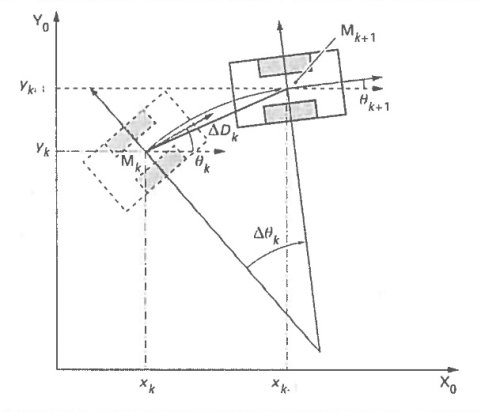
Le déplacement élémentaire ∆D et la rotation élémentaire ∆θ du robot dans le plan s’expriment en fonction des déplacements élémentaires des roues droites et gauche, respectivement ∆dd et ∆dg , par :
∆D = (∆dd + ∆dg ) /2 ∆θ = (∆dd - ∆dg ) / E
E étant la dimension de l’essieu (distance qui sépare les points de contact des deux roues avec le sol)
Désignons (xk,yk,θk) la configuration du véhicule à l’instant k, et par ∆Dk et ∆θk les composants du déplacement élémentaire mesuré entre l’instant k et k+1. Le cap à l’instant k+1 est :
θk+1 = θk + ∆θk
Pour estimer les coordonnées xk+1 et yk+1 du robot à l’instant k+1, il faut émettre des hypothèses sur la trajectoire du robot entre les deux instants d’échantillonnage. Selon les hypothèses choisies, les équations obtenues sont plus ou moins complexes.
Les formules les plus simples sont obtenues en considérant que le robot se déplace en ligne droite de ∆Dk dans la direction définie par θk, puis effectuer une rotation sur place de ∆θk.
xk+1 = xk + ∆Dk * cos(θk)
yk+1 = yk + ∆Dk * sin(θk)
En faisant l’hypothèse que la trajectoire du robot est localement assimilable à un arc de cercle de longueur ∆Dk , tangent en Mk à la direction définie par θk et en Mk+1 à la direction définie par le nouveau cap θk+1, on obtient (je vous passe les savants calculs) :
xk+1 = xk + ∆Dk * cos(θk +∆θk/2)
yk+1 = yk + ∆Dk * sin(θk +∆θk/2)
Dans le cas d’un robot possédant des odomètres les formules deviennent dans le premier cas :
∆θk = 2 π * (Rw / E ) * (T1-T2)/Tr
∆x = Rw cos (θk) (T1+T2)*π/Tr
∆y = Rw sin (θk) (T1+T2)*π/Tr
Pour le second cas :
∆x = Rw cos (θk+∆θk/2) (T1+T2)*π/Tr
∆y = Rw sin (θk+∆θk/2) (T1+T2)*π/Tr
Avec T1 nombre de ticks de l’encodeur 1 et T2 le nombre de ticks de l’encodeur 2, Rw le rayon de chaque roue, E la distance qui sépare les points de contact des deux roues avec le sol, Tr le nombre de ticks pour un tour de roue complet.
xk+1 = xk + ∆x
yk+1 = yk + ∆y
θk+1 = θk + ∆θk
Frédéric 18/10/2013
 PoBot
PoBot
 L’accostage, c’est Flou ! (Docking, its Fuzzy !)
L’accostage, c’est Flou ! (Docking, its Fuzzy !)



