3- Les déformations de l’image

Déformation par l’optique

En théorie il est possible de concevoir des lentilles avec un rayon de courbure parabolique parfait, or en pratique ce n’est pas possible à cause de problèmes matériel et technique. C’est pourquoi les lois des lentilles minces ne sont pas tout à fait respectées. Sur des objectifs haut de gamme cette déformation sera minime par contre sur des webcams la déformation sera importante car elles sont équipées de lentilles qui coutent le moins cher à usiner et sont souvent en plastique.

Cette déformation est aussi accentuée à du fait du non-respect de l’approximation de Gauss de l’optique géométrique car sur les objectifs grands angles, on ne respecte plus la propriété d’avoir des angles d’incidence des rayons faibles et un point d’incidence proche de l’axe optique. Visuellement voici à quoi ressemblent ces déformations :

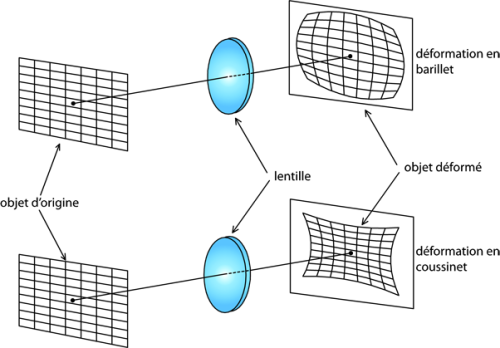
Ces déformations ne sont toutefois pas des aberrations car l’image d’un point est un point, nous travaillons dans un espace bijectif. Ainsi il est possible de construire une fonction de correction afin de replacer les points à leur véritable place sans la déformation. L’objectif étant que sur l’image corrigée des droites restent des droites.

Le modèle de correction est paramétré par 3 coefficients k1,k2 et k3. Ce modèle est dit radial car cette déformation sera calculée par rapport à la position d’un point par rapport à la position de la position du centre optique, cette distance est un rayon :

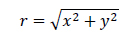
On calcule ensuite les positions corrigées des points :

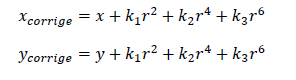
Déformation par système non-centré

Si l’axe orthogonal au plan image n’est pas colinéaire à l’axe optique alors une déformation supplémentaire se rajoute au modèle. La première conséquence va être de déformer géométriquement l’image, et la seconde conséquence sera de rendre floue une partie de l’image car cette partie ne sera pas sur la plan image focal de l’objectif.
Cependant on peut écarter la seconde conséquence dans le traitement de la déformation, car il est impossible de corriger une image floue et car dans la pratique le flou est très peu présent car la différence de parallaxe est faible.

L’origine de cette erreur de parallaxe peut être une fixation de l’objectif non fiable ou alors un mauvais positionnement du capteur à l’intérieur de la caméra (boule de colle sous le capteur).

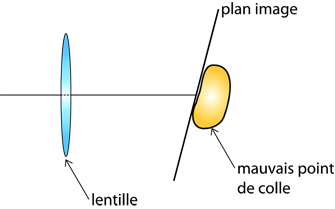
Visuellement voici ce que donne cette déformation sur l’image :

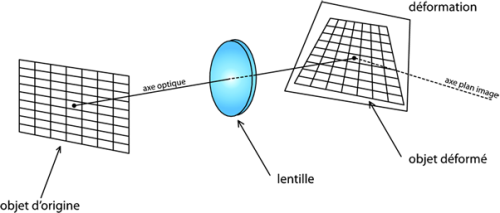
Là aussi la correction géométrique est possible par un modèle à 2 coefficients p1 et p2 :

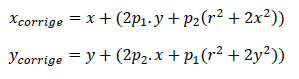
Il est à noter que ces deux corrections sont additives.

Rassurez-vous ! Vous venez de voir la majeure partie des connaissances à avoir avant de pouvoir vraiment faire de la vision. Par la suite je vous présenterai des algorithmes qui vous permettrons de calculer tout seul les coefficients que nous avons vu.

Bien entendu avec le code source fourni !