Ayant vu l’histoire et l’évolution de la caméra au cours du temps, nous pouvons maintenant nous intéresser à une meilleure compréhension scientifique de son fonctionnement (des notions en optique des lentilles minces sont nécessaires pour une meilleure assimilation de la théorie, cf http://www.web-sciences.com/optique/optique2.php ).
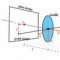
On peut synthétiser le fonctionnement d’une caméra par le schéma suivant :
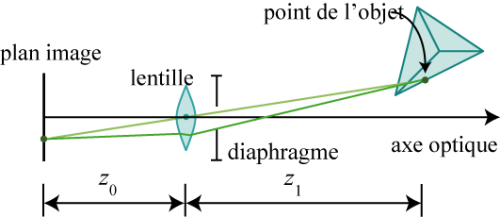
Pour rappel l’équation d’une lentille mince est :
1/|f| =1/Z0 +1/Z1
Avec f la focale de la lentille (ou focale équivalente de l’objectif).
Pour notre utilisation, nous avons fait une mise au point à l’infini (∞), nous souhaitons qu’un objet lointain apparaisse nette sur notre capteur. On a alors Z1≫Z0 , on peut donc approximer Z0= |f| d’après l’équation des lentilles minces. Physiquement cela signifie que notre plan image doit se trouver à une distance f du centre optique de la lentille.
Cette configuration particulière permet de plus d’avoir une profondeur de champ importante, ne dépendant peu de l’ouverture du diaphragme. C’est-à-dire que même un objet relativement proche de la caméra apparaîtra comme net car Z0 sera pas très éloigné de f.
Si l’on récapitule on peut établir ce modèle :
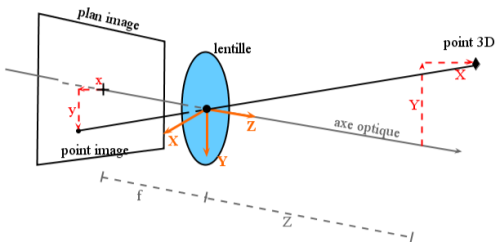
Grâce au théorème de Thalès on en déduit : f/Z=-x/X=-y/Y
Soit les équations de projection suivantes : y=-f.Y/Z ; x=-f.X/Z
Maintenant nous allons procéder à une petite astuce, qui ne change rien au résultat mais qui va nous permettre de mieux manipuler les résultats. Comme nous l’avons vu, nos axes des y et des x sont inversés par rapport à ce que l’on observe, c’est pourquoi nous allons modifier légèrement le modèle afin de faire passer le plan image "devant" le centre optique. Bien entendu, cette manipulation est physiquement impossible à réaliser, mais d’un point de vue mathématique c’est possible. Nous avons alors :
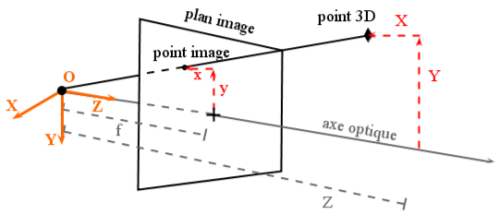
Et donc les nouvelles équations de projection : y=f.Y/Z ; x=f.X/Z
Nous venons de voir comment un point de l’espace est projeté sur un plan image, or cette projection de la 3D à la 2D nous fait perdre une information, celle de profondeur. En effet êtes-vous en mesure de me dire précisément à quelle distance se trouve un objet que vous pouvez voir sur une photo ? La réponse je la connais déjà, c’est non.
A partir de maintenant il faut bien vous mettre à l’esprit que ce que nous apercevons sur une photo, c’est un "rayon lumineux" et non un point 3D. En effet la seule chose que nous pouvons savoir c’est que ce point se trouve forcément quelque part sur la droite passant par le centre optique et le point, mais nous ne pouvons dire ou exactement. Nous allons donc faire appel à une notion que l’on appelle coordonnées homogènes et qui représente justement l’information que le point est quelque part sur cette droite. Une coordonnée homogène ne représente ni plus ni moins que le vecteur directeur de cette droite.
Il reste encore un petit changement de repère à effectuer, car nous avons calculer la position x,y par rapport au centre optique, or le centre optique ne coïncide pas au centre du repère de l’image pixelique dont nous faisons l’acquisition. Il faut établir la position du centre optique (U0,V0) par rapport au repère (U,V) de l’image. Nous allons aussi intégrer un terme α (en mètre par pixel) représentant la largeur d’un pixel dans un système métrique. En effet un pixel représente un capteur, qui possède une taille finie (sur nos caméras un pixel fait 3,4 µm de large et de hauteur). Cependant toutes les caméras ne possèdent pas des capteurs parfaits, et selon la technologie les capteurs peuvent être plus larges que hauts, donc nous allons dissocier alpha_x et alpha_(y ).
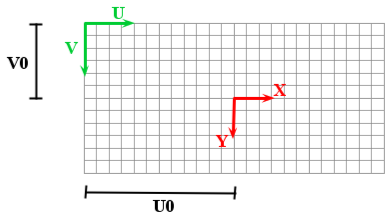
Nous avons alors :
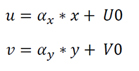
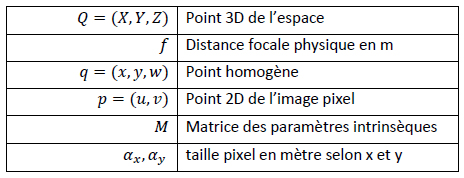
Nous allons à partir d’ici commencer à écrire tous nos calculs sous forme vectorielle afin de faciliter la représentation des calculs. N’ayez pas peur ce n’est pas parceque que le mot matrice fait peur qu’il faut quitter ce site :p Je ne complique rien, la matrice est aussi simple que les formules du dessus. Par convention voici la liste des symboles que je vais utiliser :
On introduit la matrice intrinsèque M ainsi que les calculs en points pixels :
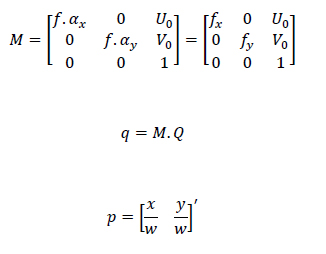
 PoBot
PoBot
 2- Modélisation
2- Modélisation